暂无测试数据。

题目描述

在数学课上，爱思的老师为每一个同学都准备了一个几何图形，图形上均匀分布着 $n$ 个点。爱思很无聊，于是决定给点涂上颜色。

具体地，初始每个点都是白色的。爱思只有铅笔，所以只能把点涂成黑色的。爱思希望对两种染色问题，分别求出其对应的方案数。

给定 $n$，请输出以下两个问题分别对应的染色方案数：

1. 现有 $n$ 个点均匀分布在一个圆周上，初始每个点都是白色。爱思希望给其中一些点染上黑色，使得任意两个相邻的黑色点的距离都相同，并且至少有一个点染上黑色。
   两个点的距离定义为从一个点沿圆周顺时针行走到另一个点的所需要经过的圆弧的段数。
   比如下图中，涂色的顶点 $1$ 到顶点 $4$ 的距离为 $3$ ，顶点 $4$ 到顶点 $1$ 的距离为 $1$ 。
   
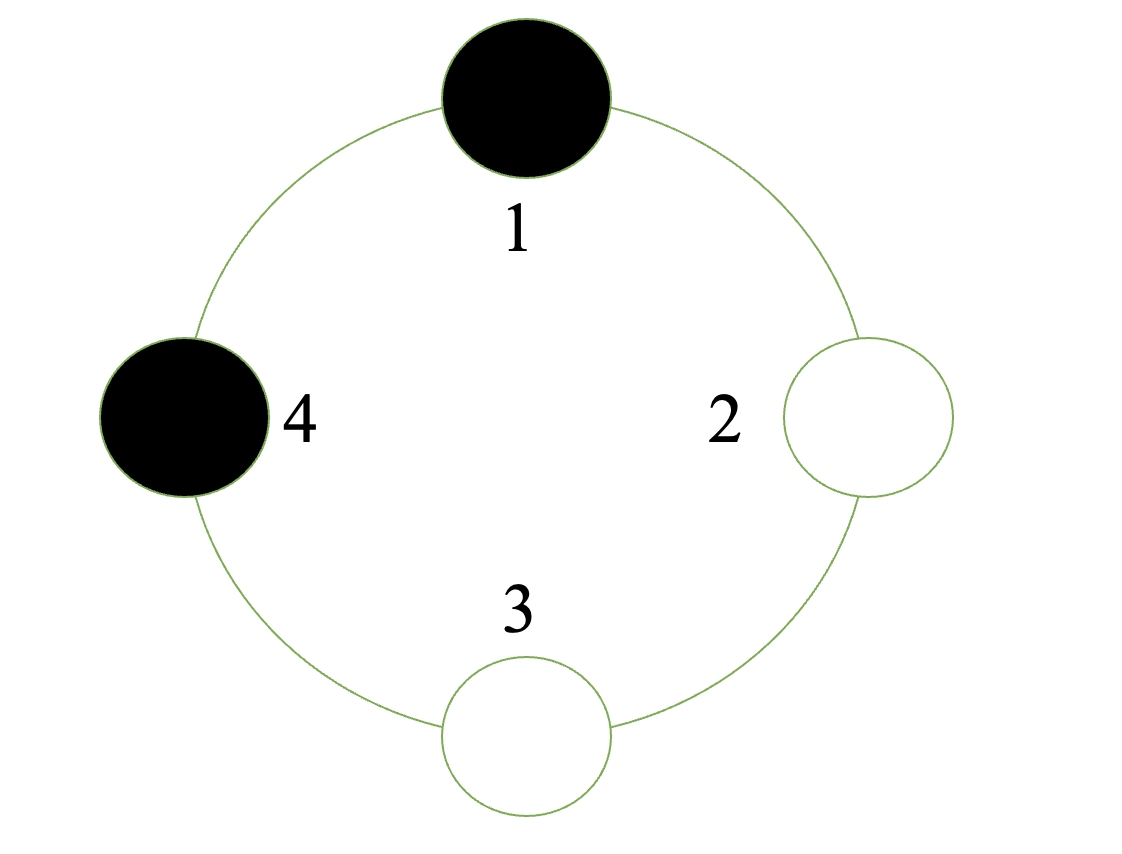
   两个染色方案不同，当且仅当有至少一个点的颜色在两个方案中不同。
   圆周不可旋转、翻转。

2. 现有 $n$ 个点均匀分布在一条线段上，初始每个点都是白色。爱思希望给其中一些点染上黑色，使得任意两个相邻的黑色点的距离都相同，并且至少有一个点染上黑色。
   两个点的距离定义为其在线段上的距离。
   比如下图中，涂色的顶点 $1$ 到顶点 $4$ 的距离为 $3$ ，顶点 $4$ 到顶点 $1$ 的距离为 $3$ 。
   

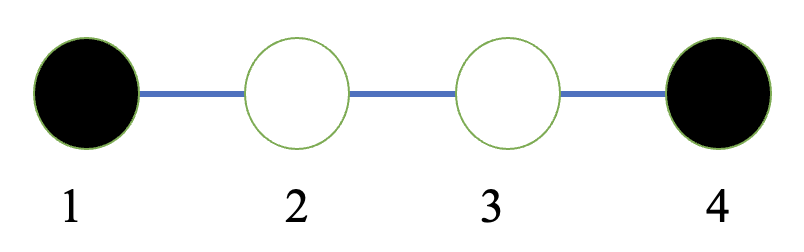
   两个染色方案不同，当且仅当有至少一个点的颜色在两个方案中不同。

输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 $T$，表示数据组数。

接下来包含 $T$ 组数据，每组数据包含一行一个整数 $n$，含义见题目描述。

输出格式

为了减少输出量，只输出一行包含两个用单个空格隔开的整数，分别表示两个问题的答案分别的异或和。

形式化地说，假设第 $i$ 组数据对应的两个问题的答案分别为 $a_i$、$b_i$，你需要输出两个数 $A$、$B$，使得 $A=\bigoplus_{i=1}^T a_i$，$B=\bigoplus_{i=1}^T b_i$，其中 $\bigoplus$ 表示二进制下按位异或。

数据范围

对于 $100\%$ 的数据，保证 $T\le 10^6，1\le n\le 10^7$。

本题共 $10$ 个测试点，各测试点详细信息见下表。

测试点编号	$T\le$	$n\le$
$1$	$10$	$10$
$2$	$10$	$10^3$
$3$	$10^6$	$10^3$
$4$	$10^6$	$10^3$
$5$	$10$	$10^6$
$6$	$10^6$	$10^6$
$7$	$10^6$	$10^6$
$8$	$10^6$	$10^7$
$9$	$10^6$	$10^7$
$10$	$10^6$	$10^7$

1
4

7 13