暂无测试数据。

蒜头君刚刚设计了 $n$ 个城市（编号为 $1\sim n$）之间高速公路的路线图，路线图可以看作一棵有根树。

修建高速公路是需要成本，最初设计时，默认按照传统方式修建高速公路，因此可以精确的计算出每段高速公路（树上的边）的成本。

首先你要计算出任意两个城市之间通过高速公路连通时的最小成本之和是多少？

现在有 $q$ 次操作，每次操作会修改某段高速公路的修建成本，同时你需要回答出修改后任意两个城市之间通过高速公路连通时的最小成本之和是多少？

输入格式

第一行输入两个整数 $n,q$，表示城市（结点）的数量和操作的次数。

接下来 $n - 1$ 行，每行三个正整数 $x, y, z$，表示结点 $x$ 是结点 $y$ 的父亲结点，按照传统方式修建这段高速公路时的成本为 $z$。

接下来 $q$ 行，每行两个正整数 $a, b$，表示将 $a$ 结点与其父亲结点之间修建高速公路的成本修改为 $b$。

数据保证结点 $1$ 为树的根结点，$a\neq 1$。

输出格式

第一行，输出一个整数，表示按照传统方式修建高速公路时，任意两个城市之间通过高速公路连通时的最小成本之和。

接下来 $q$ 行，每行输出一个整数，表示每一次修改后，任意两个城市之间通过高速公路连通时的最小成本之和。

数据范围

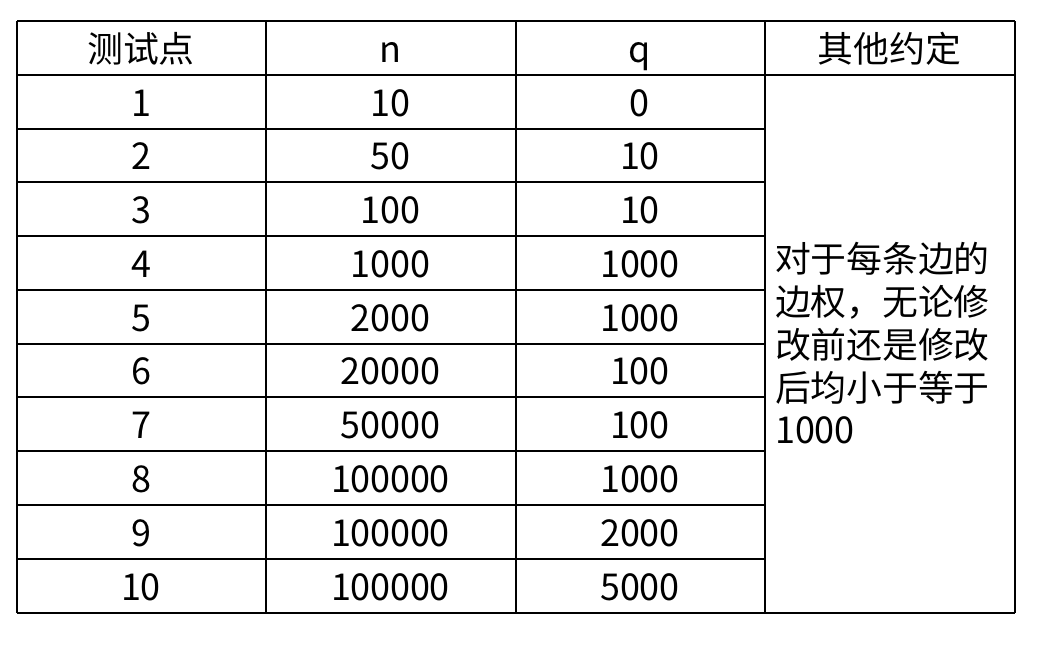
4 1
1 2 1
1 3 1
1 4 1
2 2

9
12