暂无测试数据。

P 国是远近闻名的旅游胜地，吸引了无数旅游爱好者，作为旅游爱好者的小甲和小乙自然也要去游览P国。

已知 P 国有 $n$ 座城市，且有 $n-1$ 条路将城市连通，保证城市两两之间可以相互抵达。

小甲和小乙有着不一样的旅游规划，虽然他们有不一样的起点，但是他们约定，他们最终会到达同一座城市会合。

也即小甲从 $A$ 城出发最终到达 $B$ 城，而小乙从 $C$ 城出发，最终也到达 $B$ 城。

现在，他们想知道，对于每一对旅游规划，小甲和小乙最少会经过多少个共同的城市。

输入格式

第一行输入包含三个整数， $n,q,cnt$，分别表示城市的数量，旅游规划的数量，以及测试点的编号。

测试点编号可以帮助你更好地获得部分分，你可能用不到这一则信息。

接下来 $n-1$ 行，每行包含两个整数 $u,v$ ，表示编号为 $u$ 的城市和编号为 $v$ 的城市之间存在一条通路。

接下来 $q$ 行，每行存在三个整数 $A,B,C$，表示小甲从 $A$ 城出发最终到达 $B$ 城，小乙从 $C$ 城出发最终到达 $B$ 城。

输出格式

输出 $q$ 行，每行输出一个整数，表示小甲和小乙最少共同经过的城市的数量。

数据规模与约定

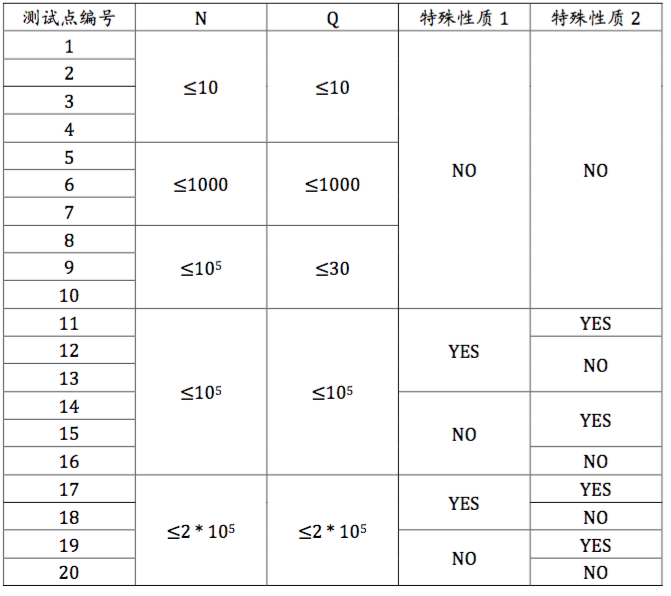
特殊性质 $1$：第 $i$ 条边连接第 $i$ 和第 $i + 1$ 个城市。

特殊性质 $2$：$A = C$。

3 3 1
1 2
2 3
1 2 3
1 1 3
3 1 3

1
1
3

4 3 2
1 2
2 3
2 4
3 2 4
3 1 4
1 2 3

1
2
1