暂无测试数据。

蒜头君有 $n$ 根竖着的滑道、$m$ 根横着的滑道。竖着的滑道在空地上并排放置，编号为 $1,2,3,\cdots,n$。每根竖着的滑道上方最初有一个小球，每个小球上有一个编号，小球的编号为当前所在竖着滑道的编号。

横着的滑道是用来连接两根相邻的竖着滑道的，不同的是，每根横着的滑道所在的高度均不相同。

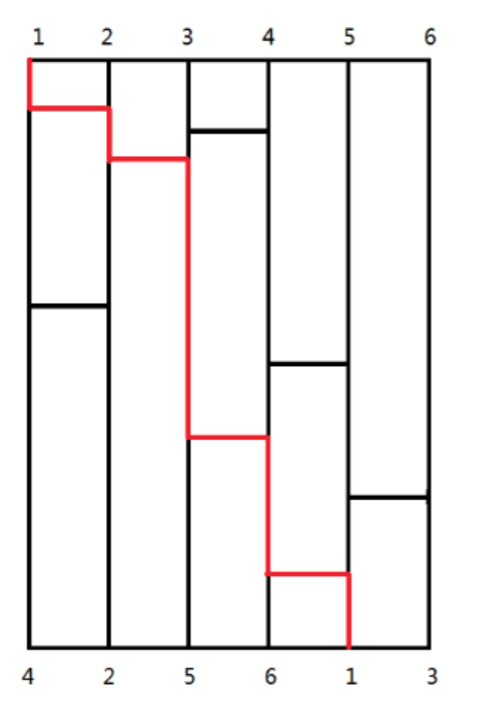
接下来小球会依次从顶端沿着竖着的滑道开始向下滑落，在滑落的过程中，如果遇到横着的滑道时，会滑向横着滑道的另一端，然后继续向下滑落，直到滑落到最低点。图中红色线表示 $1$ 号小球向下滑落的轨迹。

蒜头君想要完成两个任务：

1. 通过给定的 $n$ 根竖着的滑道和 $m$ 根横着的滑道构成的结构，求出每个小球滑落到最低点时，最底端由小球编号构成的序列，如图中的序列为：$4,2,5,6,1,3$。

2. 如果重新选择一些横着的滑道，并按照最优的方法连接两根相邻的竖着的滑道，使得获得的最终序列同样能够达到上面的效果，那么最少需要多少根横着的滑道？。

输入格式

第一行以空格隔开的两个正整数 $n,m$，表示竖着的滑道和横着的滑道的数量。

第二行 $m$ 个以空格隔开的正整数 $a_i$，依次表示从高到低的横着的滑道。数字 $a_i$ 的意义为，存在一条横着的滑道连接第 $a_i(1 \le a_i < n)$ 根竖着的滑道和第 $a_i+1$ 根竖着的滑道。

输出格式

第一行 $n$ 个以空格隔开的正整数，表示最底端由小球编号构成的最终序列。

第二行一个整数，表示最少需要多少根横着的滑道也能达到同样的效果。

数据范围

• 对于 $10\%$ 的数据：$1\leq n \le 3,1\leq m\le 5$。
• 对于 $20\%$ 的数据：$1\leq n \le 4,1\leq m \le 100$。
• 对于 $40\%$ 的数据：$1\leq n\le 8,1\leq m \le 1000$。
• 对于 $60\%$ 的数据：$1\leq n\le 1000,1\leq m \le 5000$。
• 对于 $100\%$ 的数据：$1\leq n \le 100000,1\leq m \le 1000000$。

3 3
1 2 1

3 2 1
3

6 8
1 3 2 1 4 3 5 4

4 2 5 6 1 3
8