暂无测试数据。

插入排序是一种非常常见且简单的排序算法。小 Z 是一名大一的新生，今天 H 老师刚刚在上课的时候讲了插入排序算法。

假设比较两个元素的时间为 $O(1)$，则插入排序可以以 $O(n^2)$ 的时间复杂度完成长度为 $n$ 的数组的排序。不妨假设这 $n$ 个数字分别存储在 $a_1, a_2, … , a_n$ 之中，则如下伪代码给出了插入排序算法的一种最简单的实现方式：

这下面是 C/C++ 的示范代码

for (int i = 1; i <= n; i++)
    for (int j = i; j >= 2; j‐‐)
        if (a[j] < a[j‐ 1]) {
            int t = a[j‐ 1];
            a[j‐ 1] = a[j];
            a[j] = t;
        }

这下面是 Pascal 的示范代码

for i:=1 to n do
    for j:=i downto 2 do
        if a[j]<a[j‐1] then
        begin
            t:=a[i];
            a[i]:=a[j];
            a[j]:=t;
        end;

为了帮助小 Z 更好的理解插入排序，小 Z 的老师 H 老师留下了这么一道家庭作业：

H 老师给了一个长度为 $n$ 的数组 $a$，数组下标从 $1$ 开始，并且数组中的所有元素均为非负整数。小 Z 需要支持在数组 $a$ 上的 $Q$ 次操作，操作共两种，参数分别如下：

1 x v: 这是第一种操作，会将 $a$ 的第 $x$ 个元素，也就是 $a_x$ 的值，修改为 $v$。保证 $1\leq x\leq n,1\leq v\leq 10^9$。注意这种操作会改变数组的元素，修改得到的数组会被保留，也会影响后续的操作。

2 x: 这是第二种操作，假设 H 老师按照上面的伪代码对 $a$ 数组进行排序，你需要告诉 H 老师原来 $a$ 的第 $x$ 个元素，也就是 $a_x$，在排序后的新数组所处的位置。保证 $1\leq x\leq n$。注意这种操作不会改变数组的元素，排序后的数组不会被保留，也不会影响后续的操作。

H 老师不喜欢过多的修改，所以他保证类型 $1$ 的操作次数不超过 $5000$。

小 Z 没有学过计算机竞赛，因此小 Z 并不会做这道题。他找到了你来帮助他解决这个问题。

输入格式

输入的第一行包含两个正整数 $n, Q$，表示数组长度和操作次数。保证 $1 \leq n \leq8000, 1 \leq Q \leq 2 \times 10^5$。

输入的第二行包含 $n$ 个空格分隔的非负整数，其中第 $i$ 个非负整数表示 $a_i$。保证$1 \leq a_i \leq 10^9$。

接下来 $Q$ 行，每行 $2 \sim 3$ 个正整数，表示一次操作，操作格式见题目描述。

输出格式

对于每一次类型为 $2$ 的询问，输出一行一个正整数表示答案。

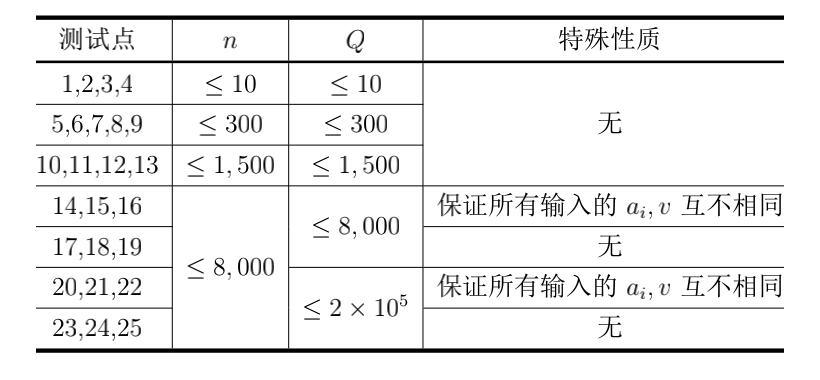
数据范围

对于所有测试数据，满足 $1 \leq n \leq 8000, 1 \leq Q \leq 2\times 10^5, 1 \leq x \leq n, 1 \leq v, a_i \leq 10^9$。

对于所有测试数据，保证在所有 $Q$ 次操作中，至多有 $5000$ 次操作属于类型一。

各测试点的附加限制及分值如下表所示。

3 4
3 2 1
2 3
1 3 2
2 2
2 3

1
1
2