#49079. 考试
考试
暂无测试数据。
马上要考试了,但蒜头君根本没有复习,所以他找到了你,想请你帮他计算出他考试所可以获得的期望分数
具体地说,试卷可以抽象成一个有向无环图,保证无重边无自环,$1$ 号节点的入度为 $0$,且第一题为 $1$ 号节点,每个节点上有两个数 $a,b$,$a$ 表示可以做对这题的概率,$b$ 表示做对这题可以获得的分值,蒜头君做的第一道题是 $1$ 号题,当一道题做对后,才能解锁它能一步到达的节点上的题,如下图:
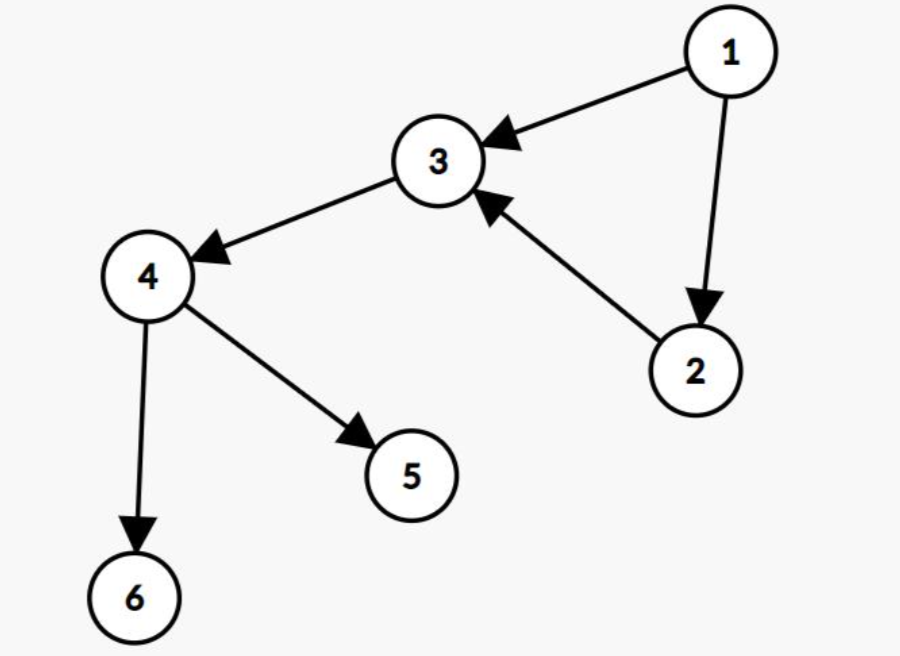
当做对 $1$ 号题的时候会解锁 $2,3$ 号题 现在给你一张“试卷”,请你帮忙算出蒜头君可以获得的期望分数
输入格式
第一行两个整数数 $n,m$,表示有 $n$ 个节点,$m$ 条边
第二行 $n$ 个不超过 $2$ 位小数的浮点数,第 $i$ 个数表示做对第 $i$ 号题的概率,保证这些数 $\leq 1$
第三行 $n$ 个整数,第 $i$ 个数表示做对第 $i$ 号题的可得的分数,保证这些数 $\leq 10^3$
接下来 $m$ 行,每行两个整数 $u,v$,表示 $u$ 号节点与 $v$ 号节点存在一条有向边,保证 $1$ 号节点入度为 $0$
输出格式
一个浮点数,表示蒜头君可以获得的期望分数,如果和标准答案的误差不超过 $10^{-3}$,即认为是通过这一测试点
数据范围与约定
| 测试点编号 | $n \leq $ | $m \leq $ | 特殊性质 |
|---|---|---|---|
| $1$ | $10$ | $5 \times 10^6$ | 给定的图为一棵有根树 |
| $2 \sim 4$ | $10^3$ | $5 \times 10^6$ | 给定的图为一棵有根树 |
| $5 \sim 8$ | $10^5$ | $5 \times 10^6$ | 给定的图为一棵有根树 |
| $9 \sim 10$ | $10^3$ | $5 \times 10^6$ | $v = u + 1$,给定的图为一棵有根树 |
| $11 \sim 12$ | $10^5$ | $5 \times 10^6$ | $u - 1$,给定的图为一棵有根树 |
| $17$ | $10$ | $5 \times 10^6$ | 无 |
| $18 \sim 19$ | $10^3$ | $5 \times 10^6$ | 无 |
| $20 \sim 25$ | $10^5$ | $5 \times 10^6$ | 无 |
4 3
0.5 0.5 1 0.5
10 20 30 40
1 2
1 3
3 4
35
undefined
undefined