暂无测试数据。

散人和 TK 是好朋友。

所谓好朋友，就是“你能够看到的只有我”，$\sout{ \text{啊不对这好像是恋人} }$。

TK 和散人一起玩完了旋转茶杯之后，他周围的事物已经虚幻了，这真是一种奇妙的感觉，于是 TK 想让全天下所有的好朋友都一起来玩旋转茶杯。

TK 一共认识 $N$ 个人，其中有些人互为好朋友，每个人都愿意为了玩旋转茶杯付出 $v_i$ 元钱(注意 $v_i$ 可能是负数，代表反给钱才玩)， TK 想选择一帮人来玩旋转茶杯，他们两两互为好朋友，并且愿意支付的总金额最大。同时为了防止一对好朋友都没有玩上旋转茶杯而蠢蠢欲动， TK 希望他没有选择的那些人中两两都不是好朋友。

TK 还想知道，他有多少种选择的方案，两个方案不同——当且仅当有至少有一个人在这两种方案中玩旋转茶杯与否的情况不同。

输入格式

第一行两个正整数 $Case$ ，$N$，分别代表测试点编号，和 TK 的朋友总数。

第二行输入 $N$ 个整数 $v_i$ ，表示第 $i$ 个朋友愿意为玩旋转茶杯支付的钱数。

为了稍稍减少输入数据量，每对朋友关系只被描述一次，具体方式如下。接下来 $N$ 行，每行开始一个非负整数 $P_i$ ，代表在第 $i+1 \sim N$ 个人 中，第 $i$ 个人的朋友有多少个，接下来 $P_i$ 个数，每个数范围在 $i+1 \sim N$ 之间，代表其中一个朋友编号。

输出格式

若 $Case$ 是偶数，则你需要输出所有合法选择中，总金额最大是多少。

若 $Case$ 是奇数，则你需要输出一共有多少种合法的选择。

数据范围

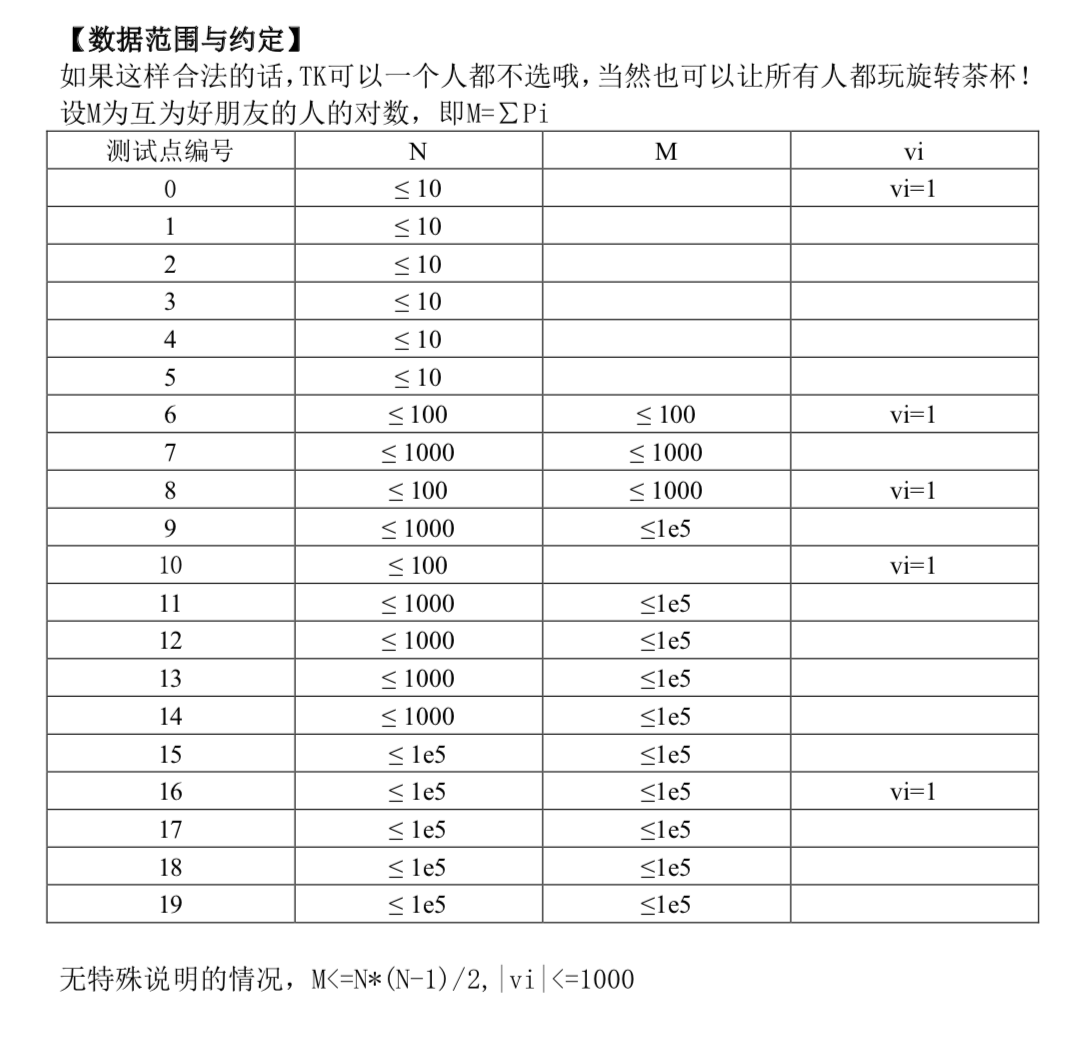
0 6
1 1 1 1 1 1
5 2 3 4 5 6
4 3 4 5 6
3 4 5 6
2 5 6
1 6
0

6

1 7
1 1 1 1 1 1 1
5 2 3 4 6 7
5 3 4 5 6 7
0
2 6 7
0
1 7
0

4