[NOI2011]道路修建
暂无测试数据。
在 W 星球上有 $n$ 个国家。为了各自国家的经济发展，他们决定在各个国家之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿意修建恰好 $n - 1$ 条双向道路。
每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端的国家个数之差的绝对值。例如,在下图中,虚线所示道路两端分别有 $2$ 个、$4$ 个国家，如果该道路长度为 $1$，则费用为 $1 \times \lvert 2 - 4 \rvert =2$。图中圆圈里的数字表示国家的编号。
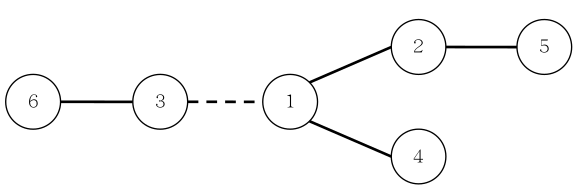
由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计算出所需要的费用。请你帮助国王们设计一个这样的软件。
输入格式
输入的第一行包含一个整数 $n$，表示 W 星球上的国家的数量，国家从 $1$ 到 $n$ 编号。
接下来 $n - 1$ 行描述道路建设情况，其中第 $i$ 行包含三个整数 $a_i$、$b_i$ 和 $c_i$，表示第 $i$ 条双向道路修建在 $a_i$ 与 $b_i$ 两个国家之间，长度为 $c_i$。
输出格式
输出一个整数，表示修建所有道路所需要的总费用。
数据范围和约定
对于所有数据，保证 $1 \le a_i, b_i \le n, 0 \le c_i \le 10^6$.
| 测试点编号 | $n=$ |
|---|---|
| 1 | $2$ |
| 2 | $10$ |
| 3 | $100$ |
| 4 | $200$ |
| 5 | $500$ |
| 6 | $600$ |
| 7 | $800$ |
| 8 | $1000$ |
| 9 | $10,000$ |
| 10 | $20,000$ |
| 11 | $50,000$ |
| 12 | $60,000$ |
| 13 | $80,000$ |
| 14 | $100,000$ |
| 15 | $600,000$ |
| 16 | $700,000$ |
| 17 | $800,000$ |
| 18 | $900,000$ |
| 19 | $1,000,000$ |
| 20 | $1,000,000$ |
6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1
20