#37366. [NOI2013]书法家
[NOI2013]书法家
暂无测试数据。
小 E 同学非常喜欢书法,他听说 NOI2013 已经开始了,想题一幅 “NOI” 的字送给大家。
小 E 有一张非常神奇的纸,纸可以用一个 $n$ 行 $m$ 列的二维方格矩阵来表示,为了描述方便,我们定义矩阵左下角方格坐标为 $(1,1)$,右上角方格坐标为 $(m, n)$。
矩阵的每个方格有一个整数的幸运值。在格子上面写字可以增加大家的幸运度,幸运度的大小恰好是所有被笔写到的方格的幸运值之和。现在你要在上面写上 N,O,I 三个字母。
下面给出 $3$ 个书法字的定义:
N 由若干($\ge 3$)个边平行于坐标轴的矩形组成,设由 $K$ 个矩形组成(标号 $1 \ldots K$),第 $i$ 个矩形的左下角方格坐标设为 $(L_i, B_i)$,右上角坐标设为 $(R_i, T_i )$,要求满足:$L_i \le R_i, B_i \le T_i$;对任意 $1 < i \le K$,有 $L_i = R_{i-1} + 1$;对任意 $3 \le i < K$,有 $B_{i-1} - 1 \le T_i \le T_{i-1}$,$B_i \le B_{i-1}$;$B_2 > B_1$,$T_2 = T_1$,$B_{K-1} = B_K$,$T_{K-1} < T_K$;
O 由一个大矩形 $A$,挖去一个小矩形 $B$ 得到,这两个矩形的边都平行于坐标轴。设大矩形 $A$ 左下角的方格坐标为 $(u, v)$,长为 $W$,宽为 $H$,则小矩形 $B$ 满足左下角方格坐标为 $(u + 1, v + 1)$,长 $W - 2$,宽 $H - 2$。要求满足:
$W \ge 3$,$H \ge 3$;$u > R_K + 1$;
I 为 $3$ 个边平行于坐标轴的从下到上的实心矩形组成,从下到上依次标号为 $1,2,3$,第 $i$ 个矩形的左下角格子坐标设为 $(P_i , Q_i )$,右上角格子坐标设为 $(G_i , H_i )$,要求满足:
$P_i \le G_i , Q_i \le H_i$;$P_1 = P_3 > u + W$,$G_1 = G_3$;$Q_1 = H_1 = Q_2 - 1, H_2 + 1 = Q_3 = H_3$;$P_1 < P_2 \le G_2 < G_1$
下图是一个 N,O,I 的例子。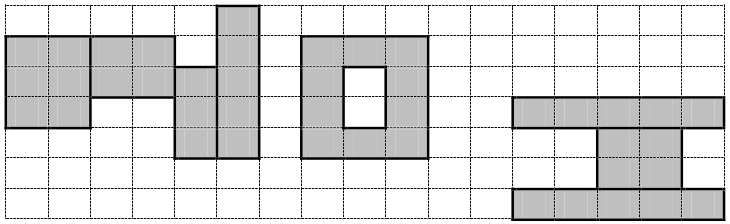
另外,所有画的图形均不允许超过纸张的边界。现在小 E 想要知道,他能画出的最大幸运度是多少。
输入格式
第一行包含两个正整数 $n$ 和 $m$ ,分别表示矩阵的行数和列数。
接下来 $n$ 行,每行有 $m$ 个整数,第 $i + 1$ 行的第 $j$ 个数表示格子 $(j, n - i + 1)$ 的幸运值。
输出格式
输出一个整数 $T$,表示小 E 能够获得的最大幸运度。
数据范围和约定
| 测试点编号 | $n$ | $m$ | 幸运值范围 |
|---|---|---|---|
| 1 | $=3$ | $=12$ | $[-50,50]$ |
| 2 | $=3$ | $=12$ | $[-50,50]$ |
| 3 | $=3$ | $=12$ | $[-50,50]$ |
| 4 | $=3$ | $=12$ | $[-50,50]$ |
| 5 | $\le10$ | $\le20$ | $[-50,50]$ |
| 6 | $\le10$ | $\le20$ | $[-50,50]$ |
| 7 | $\le10$ | $\le20$ | $[-50,50]$ |
| 8 | $\le10$ | $\le20$ | $[-50,50]$ |
| 9 | $\le150$ | $\le500$ | $=1$ |
| 10 | $\le150$ | $\le500$ | $=1$ |
| 11 | $\le80$ | $\le80$ | $=1$ |
对于所有的测试数据,保证 $n \ge 3,m \ge 12$.
3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1
24
3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-20