暂无测试数据。

丹丹是一位狂热的俄罗斯方块爱好者，但在把积分刷爆之后她终于开始感到厌倦了。于是她着手思考这样一个俄罗斯方块的简化版游戏：在初始状态地面上是空的。假设所有的积木都是长方形，且积木不能旋转或翻转。丹丹在每个时刻会选择一个位置将一块积木落下，当积木在落下的过程中碰到地面或另一块积木时，它会停留在地面上或那块积木上。落到另—块积木上意味着：上面的积木的下边界与下面的积木的上边界至少有一条线段重合(―个点不算)，如图1所示。

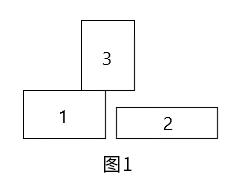
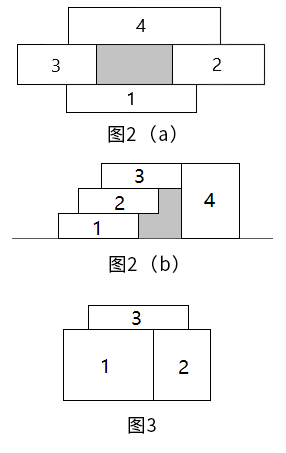
在俄罗斯方块中，如果某个时刻积木之间形成了一个洞，那么看上去就很不优美。于是丹丹想知道，每落下一块积木之后，会形成几个新的洞。一个洞是指由积木的边界或地面组成的一块面积大于0的封闭的区域，如图2（a）和图2（b）所示。

要注意的是：当出现图3所示的情况时，因为积木1和积木2紧紧地挨在一起，所以当积木3落下的时候，不会形成新的洞。

现在丹丹告诉你她依次落下的积木的髙度 $H_i$ 以及落下的位置的左右边界 $L_i$ 与 $R_i$，$1 \leq i \leq n$，而她想知道毎次积木落下时会形成几个新的洞？

输入格式

输入的第一行包含一个正整数 $n$，表示落下的积木的总数。接下来有 $n$ 行，每行有用一个空格隔开的三个整数，分别表示 $L_i$、$R_i$ 和 $H_i$ ，即积木落下的左右边界和积木的高度。

输出格式

输出 $n$ 行，每行只有一个数，第 $i$ 行表示第 $i$ 个积木落下后形成的新的洞的数目。

数据范围

输入数据保证 $0 \leq L_i < R_i \leq 100000, H_i \leq 1000$，$30\%$ 的数据保证 $n \leq 100$。$100\%$ 的数据保证 $n \leq 100000$。

6
1 3 2
4 7 2
2 5 1
3 6 1
8 11 2
6 8 3

0
0
1
0
0
2