暂无测试数据。

在 C 部落，双十字是非常重要的一个部落标志。所谓双十字，如下面两个例子，由两条水平的和一条竖直的 “1” 线段组成，要求满足以下几个限制：

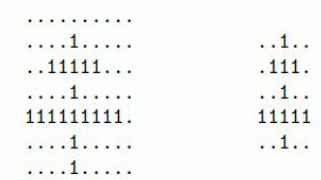
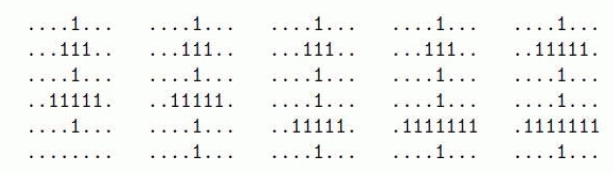
我们可以找到 $5$ 个满足条件的双十字，分别如下：

注意最终的结果可能很大，只要求输出双十字的个数 $\mod 1,000,000,009$ 的值。

• 两条水平的线段不能在相邻的两行。

• 竖直线段上端必须严格高于两条水平线段，下端必须严格低于两条水平线段。

• 竖直线段必须将两条水平线段严格划分成相等的两半。

• 上方的水平线段必须严格短于下方的水平线段。

所以上面右边的例子是满足要求的最小的双十字。

现在给定一个 $R \times C$ 的 01 矩阵，要求计算出这个 01 矩阵中有多少个双十字。

例如下面这个例子，$R=6$,$C=8$，01 矩阵如下：

输入格式

第一行为用空格隔开的两个正整数 $R$ 和 $C$，分别表示 01 矩阵的行数和列数。

输入文件第二行是一个非负整数 $N$, 表示 01 矩阵中 “0” 的个数。

接下来的 $N$ 行，每行为用空格隔开的两个正整数 $x$ 和 $y$ $(1\le x \le R,1 \le y \le C)$，表示 $(x,y)$ 是一个 “0”。数据保证 $N$ 个 “0” 的坐标两两不同。

数据保证 $R,C,N \le 10,000$, $R \times C \le 1,000,000$。(事实上 $R*C$ 可能稍大于原设定)。

输出格式

$D \mod 1,000,000,009$ 的结果，其中 $D$ 为要求的 01 矩阵中双十字的个数。

 

6  8                           

12

1  2

1  3

1  4

1  6

2  2

3  2

3  3

3  4

3  7

6  4

6  6

4  8

5