暂无测试数据。

小 A 想做一棵很大的树，但是他手上的材料有限，只好用点小技巧了。

开始，小 A 只有一棵结点数为 $ N $ 的树，结点的编号为 $ 1, 2, \ldots ,N$，其中结点 $ 1 $为根；我们称这颗树为模板树。小 A 决定通过这棵模板树来构建一颗大树。构建过程如下：

将模板树复制为初始的大树。
以下 (2.1) (2.2) (2.3) 步循环执行 $ M $ 次。 2.1. 选择两个数字 $ a, b $，其中 $ 1 \leq a \leq N, 1 \leq b \leq$ 当前大树的结点数。 2.2. 将模板树中以结点 $ a $ 为根的子树复制一遍，挂到大树中结点 $ b $ 的下方 (也就是说，模板树中的结点 $ a $ 为根的子树复制到大树中后，将成为大树中结点 $ b $ 的子树)。 2.3. 将新加入大树的结点按照在模板树中编号的顺序重新编号。例如，假设在进行 (2.2) 步之前大树有 $ L $ 个结点，模板树中以 $ a $ 为根的子树共有 $ C $ 个结点，那么新加入模板树的 $ C $ 个结点在大树中的编号将是 $ L+1, L+2, \cdots ,L+C$；大树中这 $ C $ 个结点编号的大小顺序和模板树中对应的 $ C $ 个结点的大小顺序是一致的。

下面给出一个实例。假设模板树如下图：

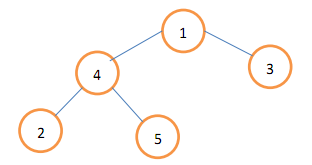
根据第 (1) 步，初始的大树与模板树是相同的。在 (2.1) 步，假设选择了 $a=4$，$b=3$。运行 (2.2) 和 (2.3) 后，得到新的大树如下图所示

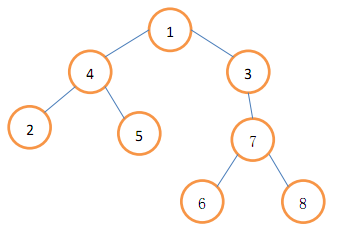
现在他想问你，树中一些结点对的距离是多少。

输入格式

第一行三个整数：$ N, M, Q $，以空格隔开，$ N $ 表示模板树结点数，$ M $ 表示第 (2) 中的循环操作的次数，$ Q $ 表示询问数量。接下来 $N-1$ 行，每行两个整数 $ \text{fr}, \text{to} $，表示模板树中的一条树边。再接下来 $ M $ 行，每行两个整数 $ x, \text{to}$，表示将模板树中 $ x $ 为根的子树复制到大树中成为结点 $ \text{to} $ 的子树的一次操作。再接下来 $ Q $ 行，每行两个整数 $ \text{fr}, \text{to}$，表示询问大树中结点 $ \text{fr} $ 和 $ \text{to}$ 之间的距离是多少。

输出格式

输出 $ Q $ 行，每行一个整数，第 $ i $ 行是第 $ i $ 个询问的答案。

数据范围和约定

对于 $100\%$ 的数据，$ N, M, Q \leq 100000 $。

5 2 3 
1 4 
1 3 
4 2 
4 5 
4 3 
3 2 
6 9 
1 8 
5 3

6
3
3