暂无测试数据。

又到暑假了，住在城市 $A$ 的 Car 想和朋友一起去城市 $B$ 旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第 $I$ 个城市中高速铁路了的单位里程价格为 $T_i$，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为 $t$。

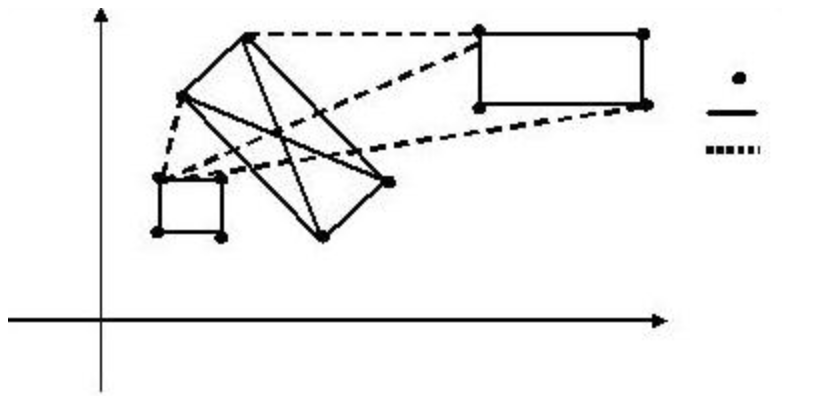
图例（从上而下）

机场

高速铁路

飞机航线

注意：图中并没有标出所有的铁路与航线。

那么 Car 应如何安排到城市 B 的路线才能尽可能的节省花费呢？她发现这并不是一个简单的问题，于是她来向你请教。

任务：找出一条从城市 $A$ 到 $B$ 的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入格式

第一行为一个正整数 $n( 0 \le n \le 10 )$ ，表示有 $n$ 组测试数据。

每组的第一行有 $4$ 个正整数 $S,t,A,B$。

$S( 0 < S \le 100 )$ 表示城市的个数，$t$ 表示飞机单位里程的价格，$A$，$B$ 分别为城市 $A$，$B$ 的序号，$(1 \le A,B \le S)$。

接下来有 $S$ 行，其中第 $i$ 行均有 $7$ 个正整数 $x_{i_1},y_{i_1},x_{i_2},y_{i_2},x_{i_3},y_{i_3},T_i$ 这当中的 $(x_{i_1},y_{i_1})$，$(x_{i_2},y_{i_2})$，$(x_{i_3},y_{i_3})$ 分别是第 $i$ 个城市中任意 $3$ 个机场的坐标，$T_i$ 为第 $i$ 个城市高速铁路单位里程的价格。

输出格式

共有 $n$ 行，每行 $1$ 个数据对应测试数据（最小花费）。保留一位小数。

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

47.5