暂无测试数据。

乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天，他突然对数的正整数次幂产生了兴趣。

众所周知，$2$ 的正整数次幂最后一位数总是不断的在重复 $2$，$4$，$8$，$6$，$2$，$4$，$8$，$6$，$\cdots$ 我们说 $2$ 的正整数次幂最后一位的循环长度是 $4$（实际上 $4$ 的倍数都可以说是循环长度，但我们只考虑最小的循环长度）。类似的，其余的数字的正整数次幂最后一位数也有类似的循环现象：

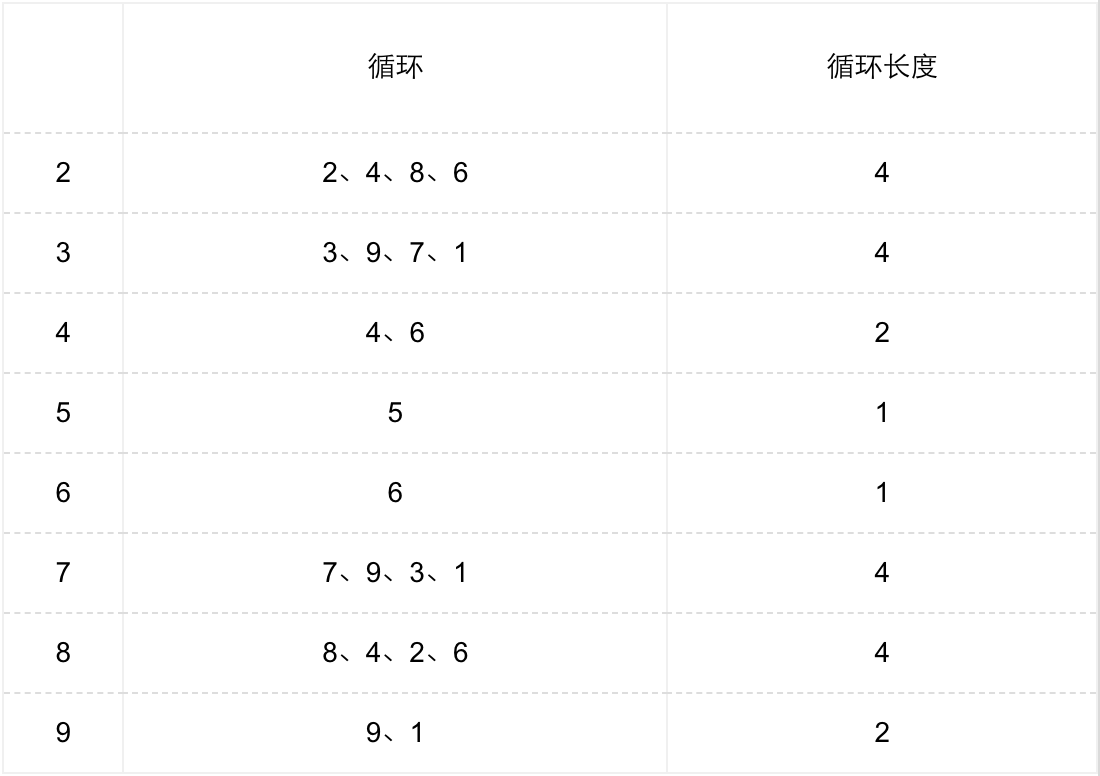
这时乐乐的问题就出来了：是不是只有最后一位才有这样的循环呢？对于一个整数 $n$ 的正整数次幂来说，它的后 $k$ 位是否会发生循环？如果循环的话，循环长度是多少呢？

注意：

1. 如果 $n$ 的某个正整数次幂的位数不足 $k$，那么不足的高位看做是 $0$。
2. 如果循环长度是 $L$，那么说明对于任意的正整数 $a$，$n$ 的 $a$ 次幂和 $a + L$ 次幂的最后 $k$ 位都相同。

输入格式

只有一行，包含两个整数 $n$（$1 \le n<10100$）和 $k$（$1 \le k \le 100$），$n$ 和 $k$ 之间用一个空格隔开，表示要求 $n$ 的正整数次幂的最后 $k$ 位的循环长度。

输出格式

包括一行，这一行只包含一个整数，表示循环长度。如果循环不存在，输出 $- 1$。

数据范围

对于 $30\%$ 的数据，$k \le 4$；

对于全部的数据，$k \le 100$。

32 2

4