暂无测试数据。

Z 国有 $n$ 座城市，$n - 1$ 条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。

Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件:

• 一座城市可以驻扎一支军队，也可以不驻扎军队。
• 由道路直接连接的两座城市中至少要有一座城市驻扎军队。
• 在城市里驻扎军队会产生花费，在编号为 $i$ 的城市中驻扎军队的花费是 $p_i$。

小 Z 很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小 Z 提出了 $m$ 个要求，每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一给出回答。具体而言，如果国王提出的第 $j$ 个要求能够满足上述驻扎条件(不需要考虑第 $j$ 个要求之外的其它要求)，则需要给出在此要求前提下驻扎军队的最小开销。如果国王提出的第 $j$ 个要求无法满足，则需要输出 $-1\ (1 \le j \le m)$。现在请你来帮助小 Z。

输入格式

第 $1$ 行包含两个正整数 $n,m$ 和一个字符串 $type$，分别表示城市数、要求数和数据类型。$type$ 是一个由大写字母A，B或C和一个数字1，2，3组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中有具体的描述。

第 $2$ 行 $n$ 个整数 $p_i$，表示编号 $i$ 的城市中驻扎军队的花费。

接下来 $n-1$ 行，每行两个正整数 $u, v$，表示有一条 $u$ 到 $v$ 的双向道路。

接下来 $m$ 行，第 $j$ 行四个整数$a, x, b, y(a \neq b)$，表示第 $j$ 个要求是在城市 $a$ 驻扎 $x$ 支军队，在城市 $b$ 驻扎 $y$ 支军队。其中，$x$、$y$ 的取值只有 $0$ 或 $1$:若 $x$ 为 $0$，表示城市 $a$ 不得驻扎军队，若 $x$ 为 1，表示城市 $a$ 必须驻扎军队;若 $y$ 为 $0$，表示城市 $b$ 不得驻扎军队，若 $y$ 为 $1$，表示城市 $b$ 必须驻扎军队。

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

输出格式

输出共 $m$ 行，每行包含 $1$ 个整数，第 $j$ 行表示在满足国王第 $j$ 个要求时的最小开销，如果无法满足国王的第 $j$ 个要求，则该行输出 $-1$。

数据范围

对于 $100\%$ 的数据，$n, m \le 300000$，$1 \le p_i \le 100000$。

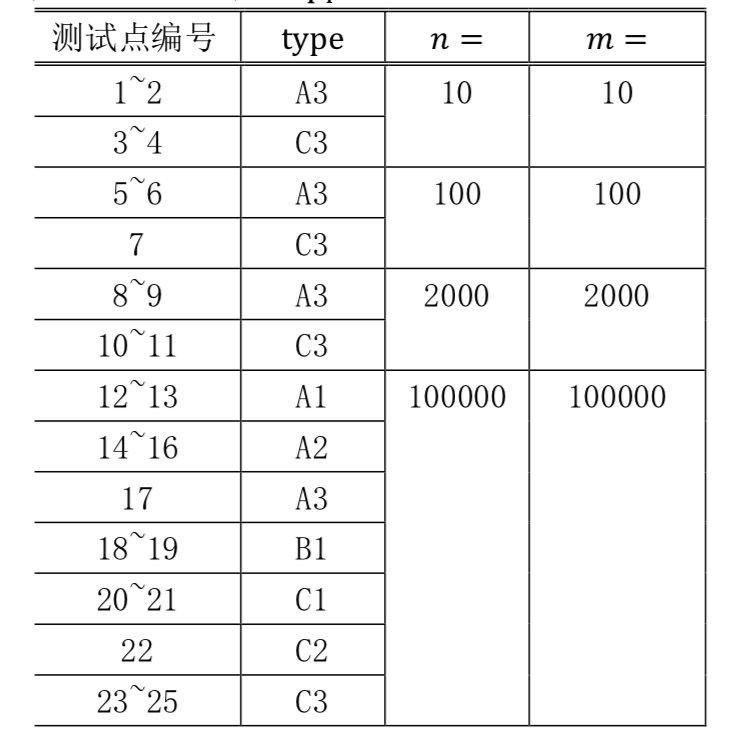
数据类型的含义:

• A: 城市 $i$ 与城市 $i+1$ 直接相连。
• B: 任意城市与城市 $1$ 的距离不超过 $100$(距离定义为最短路径上边的数量)，即如果这棵树以 $1$ 号城市为根，深度不超过 $100$。
• C: 在树的形态上无特殊约束。
• 1: 询问时保证 $a = 1, x = 1$，即要求在城市 $1$ 驻军。对 $b, y$ 没有限制。
• 2: 询问时保证 $a, b$ 是相邻的(由一条道路直接连通)。
• 3: 在询问上无特殊约束。

10 10 C3
57306 99217 65626 23866 84701 6623 7241 88154 33959 17847
2 1
3 1
4 1
5 2
6 3
7 5
8 7
9 6
10 7
4 1 9 1
3 1 2 1
3 1 4 1
3 0 10 0
6 0 9 0
3 1 7 1
7 0 10 1
5 1 1 1
10 1 4 0
1 0 4 0

213696
202573
202573
155871
-1
202573
254631
155871
173718
-1

undefined

undefined