暂无测试数据。

从前有一个间谍组织，一共派遣了 $n$ 个人潜伏在 E 国刺探情报。为了防止情报泄露，一个间谍可能只认识其他几个人。

认识的人之间有上下级的关系，并且只有一个头目为 $1$ 号，也就是说他们的关系形成了一棵有根树的结构，每个人既可以向直接上级传递情报，也可以向直接下级传递情报。一个人拿到情报后需要一天的处理时间才能传递这个情报，传递情报的时间忽略不计。

因为各种各样的突发情况，头目可能会变更，或者两个人之间暂时联系不上了。

现在给出 $m$ 个突发事件：可能是头目发生了变更；或者是一个人拿到了情报，但他到头目的传递过程中有两个人之间失去了联系。求他把情报传给所有能接收到的人手里的时间。

注意，第一个人拿到情报的人不需要处理情报，其他人拿到情报后处理完才算接收完情报。更换头目是永久的，会影响后面的查询；失去联系是暂时的，仅影响当前查询，不影响后面的查询。

输入格式

第一行输入一个整数 $n$，表示有 $n$ 个人。

接下来 $n-1$ 行，每行两个整数 $x$ 和 $y$，表示 $x$ 与 $y$ 之间相互认识。

接下来一行，输入一个整数 $m$，表示有 $m$ 个事件。

接下来 $m$ 行，如果是C x，表示 $x$ 变成了头目。如果是Q x y，则说明 $x$ 拿到了情报，并且他向上第 $y-1$ 级上级与向上第 $y$ 级上级之间的联系暂时断掉了，如果他没有第 $y$ 级上级，那么这条限制就没有用。他的直接上级是第 $1$ 级上级。你需要计算把情报传递给所有能接收到的人手里的时间。

输出格式

对于每个 $Q$，输出把情报传给所有能接收到的人手里的时间。

数据范围

对于 $20\%$ 的数据：$n,m \le 3000$。

对于另外 $20\%$ 的数据：保证是一条链。

对于另外 $30\%$ 的数据：头目不会变更。

对于 $100\%$ 的数据：$n,m \le 200000$，$y \ge 1$。

样例解释

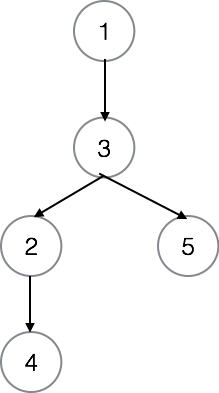
初始的图如上。

Q 4 1 的时候，2 - 4 之间的联系断了，这样消息从 $4$ 传不出去，时间为 $0$。

Q 4 2 的时候，2 - 3 之间的联系断了，$4$ 只需要把消息传给 $2$ 就好了，需要一天的时间。

Q 4 3 的时候，1 - 3 之间的联系断了，一共需要 $3$ 天的时间。

C 2 把头目换成了 $2$。

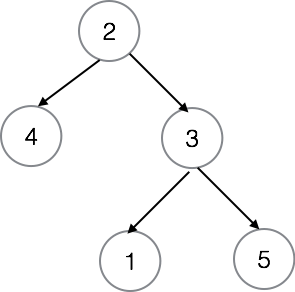
Q 1 2 的时候，2 - 3 之间的联系断了，传给所有人一共需要 $2$ 天的时间。

Q 1 3 的时候，没有人失去联系，传给所有人一共需要 $3$ 天的时间。

5
1 3
2 4
3 2
3 5
6
Q 4 1
Q 4 2
Q 4 3
C 2
Q 1 2
Q 1 3

0
1
3
2
3