暂无测试数据。

给 $n$ 个人安排座位，先给每个人一个 $1$~$n$ 的数，设第 $i$ 个人拿到的数为 $a_i$（不同人拿到的数可能相同）。接下来，从第一个人开始，大家依次入座，第 $i$ 个人来了以后尝试坐到 $a_i$（座位编号依次为 $1\ldots n$），如果 $a_i$ 被占据了，就尝试 $a_i+1$，$a_i+1$ 也被占据了的话就尝试 $a_i+2$，以此类推，如果一直尝试到编号为 $n$ 的座位也不行，则该安排方案就不合法。

现在，有 $m$ 个人拿到的数已经确定（他们或许贿赂了你的上司……），你只能安排剩下的人的数，求最后有多少种不同的可能的合法座位分配方案（注意，这里是最后的座位方案，两个座位方案之间只要有一个位置坐的不是同一个人就是不同的座位方案）。由于答案可能很大，只需输出其除以 $M$ 后的余数即可。

输入格式

第一行输入三个整数 $n,m,M$。

若 $m$ 不为 $0$，则接下来输入 $m$ 行，每行输入两个正整数 $p_i, q_i$。表示第 $p_i$ 个人拿到的数必须为 $q_i$，保证输入的 $p_i$ 不会重复。

输出格式

输出一个整数，表示不同的方案数。

数据范围

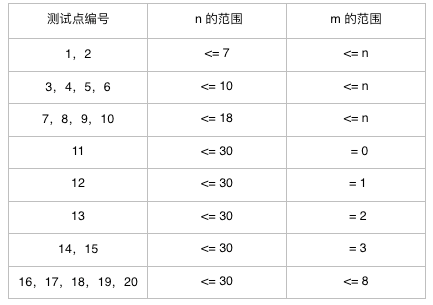
所有数据满足 $M \le 10^9$，且 $m \le n$，$1 \le p_i, q_i \le n$。

样例解释

对于样例 $1$，前面 $3$ 个人都已经分配了，正好填满 $1,2,3$，那么对于第 $4$ 个人，无论选什么都会坐到 $4$ 号位置上，所以有 $1$ 种方案。

样例 $2$，有 $3$ 个人固定了，$2$ 坐在 $9$ 号，$5$ 坐在 $10$ 号，$7$ 想坐在 $9$ 号，但是有人，依次顺延，$10$ 号也有人，所以没有可行的安排方案了。

4 3 10
1 2
2 1
3 1

1

10 3 8882
7 9
2 9
5 10

0

7 3 401574734
3 3
1 7
5 4

48