暂无测试数据。

伦伦刚刚在高中学习了解析几何，学会了计算两条直线的交点。这天，老师给她布置了一道作业。在平面上有 $n$ 条直线，他们之间有若干交点。给定一对平板（两条平行的直线），问这有多少对直线，他们的交点在这一对平板之间（注意 $(i, j) 和 (j, i) 只算一对$）。

输入格式

第一行三个整数 $k,a,b$ 表示平板的两条平行直线的方程为 $y=kx+a$ 和 $y=kx+b$，保证 $a<b$。

第二行一个整数 $n$。

接下来 $n$ 行每行两个整数 $k_i,b_i$ 表示第 $i$ 条直线的方程 $y=k_ix+b_i$。

输出格式

一个整数，表示有多少对直线，他们的交点在平板之间。

数据范围与约定

对于 $30\%$ 的数据，$n\le 5000$。

对于 $100\%$ 的数据，$n \le 100000$。

为了简单起见，输入数据保证，没有直线和平板平行，没有两条直线的交点在平板上。

样例解释

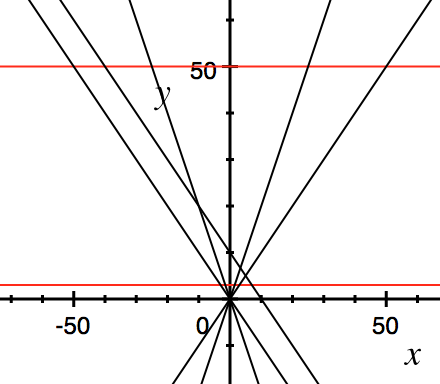
只有 $y=-x+10$ 这条直线和 $y=x,y=2x,y=-2x$ 这三条直线的交点在区域内。

0 3 50
5
1 0
2 0
-1 0
-2 0
-1 10

3