暂无测试数据。

小 $T$ 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 $n$ 个矿石，从 $1$ 到 $n$ 逐一编号，每个矿石都有自己的重量 $w_i$ 以及价值 $v_i$。检验矿产的流程是：

1. 给定 $m$ 个区间 $[L_i,R_i]$。
2. 选出一个参数 $W$。
3. 对于一个区间 $[L_i,R_i]$，计算矿石在这个区间上的检验值 $Y_i$：

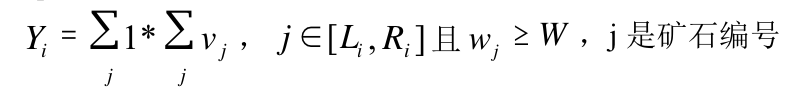
这批矿产的检验结果 $Y$ 为各个区间的检验值之和。即：$Y=\sum_{i=1}^m Y_i$。

若这批矿产的检验结果与所给标准值 $S$ 相差太多，就需要再去检验另一批矿产。小 $T$ 不想费时间去检验另一批矿产，所以他想通过调整参数 $W$ 的值，让检验结果尽可能的靠近标准值 $S$，即使得 $S-Y$ 的绝对值最小。请你帮忙求出这个最小值。

输入格式

第一行包含三个整数 $n,m,S$，分别表示矿石的个数、区间的个数和标准值。

接下来的 $n$ 行，每行 $2$ 个整数，中间用空格隔开，第 $i+1$ 行表示 $i$ 号矿石的重量 $w_i$ 和价值 $v_i$。

接下来的 $m$ 行，表示区间，每行 $2$ 个整数，中间用空格隔开，第 $i+n+1$ 行表示区间 $[L_i,R_i]$ 的两个端点 $L_i$ 和 $R_i$。注意：不同区间可能重合或相互重叠。

输出格式

表示所求的最小值。

数据范围

对于 $10\%$ 的数据，有 $1 \le n, m \le 10$。

对于 $30\%$ 的数据，有 $1\le n, m \le 500$。

对于 $50\%$ 的数据，有 $1\le n,m \le 5000$。

对于 $70\%$ 的数据，有 $1\le n,m \le 10000$。

对于 $100\%$ 的数据，有 $1 \le n,m \le 200000$，$0 < w_i,v_i \le 10^6$，$0 < S \le 10^{12}$，$1\le L_i \le R_i \le n$。

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3

10