暂无测试数据。

凡终于发愤图强，决定专心搞 OI，不再玩纸牌和坑钱了！没过多久就飘飘然了，总是陷入自己进了集训队的深黑幻想之中。

样听说了之后，决定考一考凡欧拉回路怎么写。

样：“我给你出一道题啊，是欧拉回路的，有 $N$ 个点......”。

凡：“欧拉回路有什么卵用？你看 Epacs 不会写也能进集训队！”。

样：“他不会写欧拉回路，但他会做题啊，比如说这道题......”。

“有 $N$ 个点，$M$ 条奇怪的单向边，每个边有三个参数 $A_i$，$B_i$，$C_i$，你可以指定这条边是从 $A_i$ 连向 $B_i$ 还是从 $A_i$ 连向 $C_i$，要求你构造一种方案使得把这 $M$ 条边都指定完了之后，每个点的出度和入度相等！”。

凡：“这题我会做啊，但是这 tmd 和欧拉回路有什么关系？！”

输入格式

第一行两个正整数 $N$，$M$，表示点的数目与边的数目。

接下来 $M$ 行，每行三个正整数，代表 $A_i$，$B_i$，$C_i$，含义如题目中所示。

输出格式

输出一个长度为 $M$ 的由 $01$ 组成的字符串代表一个合法解。

其中第 $i$ 个位置为 $0$ 代表 $A_i$ 向 $B_i$ 连边，为 $1$ 代表 $A_i$ 向 $C_i$ 连边。

如果有多组解，输出任意一组即可，保证存在合法解。

数据范围与约定

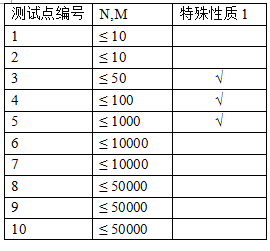
特殊性质 1: 保证所有的 $C_i=B_i+1$。

对于所有数据，保证 $1\le A_i,B_i,C_i\le N$，但是不保证 $A_i$，$B_i$，$C_i$ 互不相同。

3 2
1 2 3
2 1 3

00